Chapter summary

The efficiency of competition should be a result familiar from intermediate microceconomics. This chapter provides a brief reminder of the role and nature of competition and demonstrates the efficiency result in both an exchange economy and in an economy with production. The role of prices is stressed since prices are the signals which guide the decisions of firms and consumers and determine the relative values of different goods and services. Prices are also crucial in the attainment of economic efficiency.

2.1 The exchange economy

This model of the economy considers the simplest form of economic activity: the exchange of two commodities between two parties in order to obtain mutual advantage.

The two consumers are labelled 1 and 2 and each has an initial stock, or endowment, of the economy’s two goods. The consumers exchange quantities of the two commodities in order to achieve consumption levels that are preferred to the initial endowments. The rate at which one commodity can be exchanged for the other is determined by the market prices.

The endowment of consumer h, h = 1,2, is denoted by w^h = (w_1^h, w_2^h), where w_1^h > 0 and h's initial stock of good i, i = 1, 2. With prices p_1 and p_2, a consumption plan for consumer h, x^h(x_1^h, x_2^h) is affordable if it satisfies the budget constraint p_1 x_1^h + p_2^h = p_1 w_1^h + p_2 w_2^h

Consumer h chooses the consumption plan that maximises their utility function

U^h = U^h (x_1^h x_2^h)

In equilibrium, the total consumption of the two consumers must equal the available stock of the goods. A pair of consumption plans for the two consumers that maximises utility and satisfies this requirement is called an equilibrium for the economy.

2.2 The Edgeworth box

The diagram is constructed by noting that the set of consumption plans that are possible given the endowments can be represented as points in a rectangle with sides of length w_1^1 + w_2^1 and w_1^2 + w_2^2. In this rectangle the south-west corner can be treated as the zero consumption point for consumer 1 and the north-east corner as the zero consumption point for consumer 2. The consumption of good 1 for consumer 1 is then measured horizontally from the south-west corner and for consumer 2 horizontally from the north-east corner. Measurements for good 2 are made vertically.

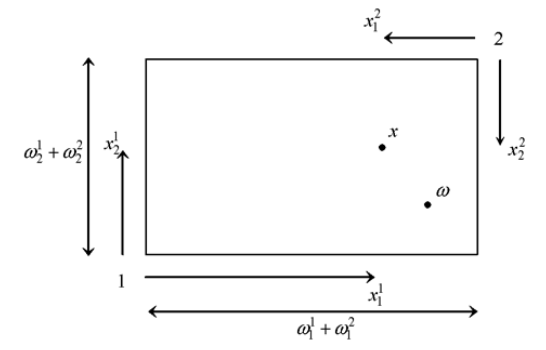
The Edgeworth box is completed by adding the preferences of the consumers and the budget constraints. The indifference curves of consumer 1 are drawn relative to the south-west corner and those of consumer 2 relative to the north- east corner. From (2.1), it can be seen that the budget constraint of consumer h must pass through the endowment point. Since the endowment point is common to both consumers, a single budget line through the endowment point with gradient p 1 /p 2 captures their market opportunities.

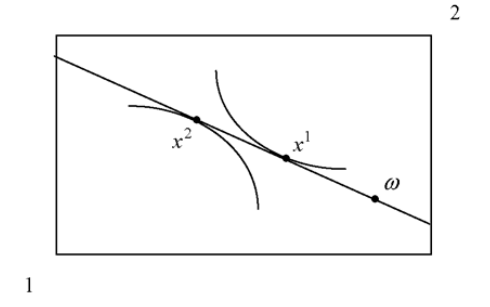
2.3 Equilibrium

An equilibrium of the economy is a position where supply is equated to demand. This is assumed to be achieved via the adjustment of prices. The prices at which supply is equal to demand are called equilibrium prices.

Equilibrium is achieved when the prices are such that the indifference curves of the consumers have a common point of tangency on the budget line.

2.4 Normalisations and Walras’ law

It has already been noted that the budget constraint always passes through the endowment point and its gradient is determined by the price ratio. The consequence of this is that only relative prices matter, rather than the absolute level, in determining demands and supplies.

The explanation for this result is that consumers are only concerned with the real purchasing power embodied in their endowment and not in the price level itself. Since their nominal income is equal to the value of the endowment, any change in the level of prices raises nominal income just as much as it raises the cost of purchases. This leaves real incomes unchanged.

The first implication of this is that the model cannot determine the level of prices. This indeterminacy is removed by adopting a price normalisation which is a method of fixing a scale for prices. The simplest way to do this is to select a commodity as numeraire, which means that its price is fixed at 1 and all other prices are measured relative to this. The numeraire chosen in this way can be thought of as the unit of account for the economy.

Walras’ law has a further implication. Since p_1 Z_1 + p_2 Z+2 = 0, if Z_1 = 0 then Z 2 = 0 (and vice versa). That is, if demand is equal to supply for good 1 then demand must also equal supply for good 2. Equilibrium in one market necessarily implies equilibrium in the other. This observation allows the construction of a simple diagram to illustrate equilibrium.

2.5 Pareto efficiency

In an economy with two or more consumers there will be a divergence of views on the most preferred allocation. To resolve this divergence it is necessary to construct a test of efficiency that can accommodate differences in preferences.

To achieve this, economists employ the concept of Pareto efficiency. Pareto efficiency judges an allocation by considering whether it is possible to undertake a reallocation of resources that can benefit at least one consumer without harming any other. If no such improving reallocation can be found, then the initial position is deemed to be Pareto efficient. An allocation that satisfies this test can be viewed as having achieved an efficient distribution of resources.

2.6 Exchange efficiency

It is surprising enough that prices can always be found which simultaneously equate demand and supply for all goods. What is even more remarkable is that the equilibrium obtained is efficient.

The welfare properties of the economy, which are called the Two Theorems of welfare economics, are the basis for claims concerning the desirability of the competitive outcome. In brief, the First Theorem states that a competitive equilibrium is Pareto efficient and the Second Theorem that any Pareto efficient allocation can be decentralised as a competitive equilibrium.

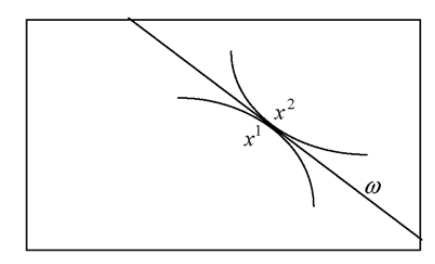
For a two consumer exchange economy, the First Theorem can be demonstrated by using an Edgeworth box diagram... the Pareto efficient allocations are given by the tangencies of the indifference curves. There are many such points and the locus of tangencies is called the contract curve. A competitive equilibrium is given by a price line through the initial endowment point, w , which is tangential to both indifference curves at the same point. Such an equilibrium is indicated by point e.

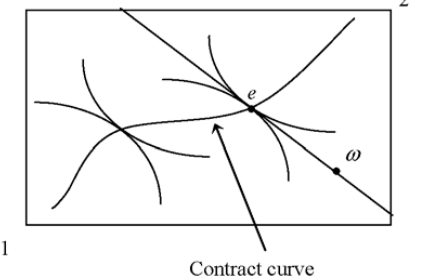
It is clear that there is no other point which is preferred by both consumers to point e. If a move is made in any direction from e one or both of the consumers must move onto a lower indifference curve. Since any change must make at least one consumer worse-off, the equilibrium is Pareto
efficient. Stating this formally: First Theorem of welfare economics: A competitive equilibrium is Pareto efficient.

The gradient of an indifference curve is defined as the ratio of the marginal utility of good 1 divided by the marginal utility of good 2 and is termed the marginal rate of substitution.

It should be noted that point e is not the only Pareto efficient allocation. All points on the contract curve are Pareto efficient since they are defined by a tangency between indifference curves. The only special feature of e is that it is the allocation reached through trading from the initial
endowment point w . If w were different, then another Pareto efficient allocation would be achieved

The Second Theorem is concerned with whether a given Pareto efficient allocation can be made into a competitive equilibrium by choosing a suitable location for the initial endowment. In the Edgeworth box, this involves being able to choose any point on the contract curve and turning it into a competitive equilibrium – this is called the process of decentralisation.

Second Theorem of welfare economics: Suppose that an allocation is Pareto efficient. Then, with convex preferences, there exists a set of prices such that the allocation is a competitive equilibrium given those prices.

2.7 Lump-sum taxation

It is implicit in the proof of the Second Theorem that the consumers are given sufficient income to purchase the Pareto efficient commodity bundles.... Any practical value of the Second Theorem depends on the possibility of achieving these required income levels. The way in which the Theorem sees this as being done is by making what are called lump-sum transfers between consumers. Quantities of endowments and profit shares are transferred between consumers to ensure the necessary income levels.

Lump-sum taxes have a central role in public economics due to their efficiency in achieving distributional objectives. The economy’s total endowment is not reduced by the application of the lump-sum taxes. This point applies to lump-sum taxes in general. There are no resources lost due to the imposition of lump-sum taxes and redistribution is achieved with no efficiency cost. In short, if they can be employed in the manner described they are the perfect taxes.

2.8 Firms

A firm is described by its production set, Y, which summarises the production technology it has available. A production technology can be thought of as a list of ways that the firm can turn inputs into outputs.

Profit maximisation can be displayed by constructing the isoprofit curves for the firm. Given a set of prices, an isoprofit curve shows all the production plans that achieve a given level of profit.

Higher isoprofit curves then represent higher levels of profit. Curves below the zero profit one represent negative profits. The firm then maximises profit at the point where its production set reaches the highest attainable isoprofit curve.

2.9 Equilibrium with production

An economy with production consists of consumers and firms. The firms use inputs to produce outputs in order to maximise their profits. Each has available a production technology which describes the ways in which it can use inputs to produce outputs. The consumers hold shares in the firms and
profits are distributed in proportion to the shareholdings. The consumers receive income from the sale of their initial endowments of goods and from the dividends from firms. When the economy is competitive both firms and consumers treat prices as outside of their control.

2.10 Efficiency with production

The extension of the two welfare theorems to an economy with production is straightforward. The major effect of production is to make supply variable: it is now the sum of the initial endowment plus the net outputs.

Reading

Chapter 6: Competitive Economies

An essential consideration in the choice of the level of detail for a model is that its equilibrium must demonstrate a dependence upon policy that gives insight into the functioning of the actual economy. p103

"The model of the exchange economy considers the simplest form of economic activity: the trade of commodities between two parties in order to obtain mutual advantage." p104

"Any pair of consumption choices that satisfies this requirement is called a feasible plan for the economy. A plan for the economy is feasible if the consumption levels can be satisfied by the value of the endowments, so

x_i^1 + x_i^2 = ω_i^1 + ω_i^2, i = 1, 2." p105

"The diagram constructed in this way is called an *Edgeworth box* ... It should be noted that the method of construction results in the initial endowment point, marked ω, being the initial endowment point for both consumers... The Edgeworth box is completed by adding the preferences and budget constraints of the consumers. The indifference curves of consumer 1 are drawn relative to the south-west corner and those of consumer 2 relative to the north-east corner" p105

"Walras’ Law .... states that the value of excess demand is zero." p110

"Walras’ Law implies that the equilibrium equations are interdependent. Since p_1Z_1 + p_2Z_2 = 0, if Z_1 = 0 then Z_2 = 0 (and vice versa). That is, if demand is equal to supply for good 1 then demand must also equal supply for good 2. Equilibrium in one market necessarily implies equilibrium in the other." p110

Wikipedia
---------
Walras's law is a principle in general equilibrium theory asserting that budget constraints imply that the values of excess demand (or, conversely, excess market supplies) must sum to zero.

Walras's law states that the sum of the values of excess demands across all markets must equal zero, whether or not the economy is in a general equilibrium. This implies that if positive excess demand exists in one market, negative excess demand must exist in some other market. Thus, if all markets but one are in equilibrium, then that last market must also be in equilibrium.

It follows that the market value of total excess demand in the economy must be zero, which is the statement of Walras's law. Walras's law implies that if there are n markets and n – 1 of these are in equilibrium, then the last market must also be in equilibrium, a property which is essential in the proof of the existence of equilibrium.

https://en.wikipedia.org/wiki/Walras%27s_law)

Chapter 7: Efficiency of Competition

"A *first-best* outcome is achieved when only the production technology and limitations on endowments restrict the choice of the decision maker. Essentially, the first-best is what would be chosen by an omniscient planner with complete command over resources. A *second-best* arises whenever constraints other than technology and resources are placed upon what the planner can do. Such constraints could be limits on income distribution or an inability to remove monopoly power." p122

"With a single consumer there is no doubt as to what is good and bad from a social perspective: the single individual’s preferences can be taken as the social preferences. To do otherwise would be to deny the validity of the consumer’s judgements." p122 Robinson Crusoe economy

"The first-best outcome for the single-consumer economy achieves the highest indifference curve possible subject to the restriction that it is feasible under the technology." p123

"Using subscripts to denote the marginal utilities of the two goods, the marginal rate of substitution is given by MRS_1,2 = U_1/U_2. Similarly, the gradient of the production possibility set is termed the marginal rate of transformation and denoted MRT_1,2 ." p123

(Marginal Rate of Transformation: how many units of good x have to stop being produced in order to produce an extra unit of good y)
(Marginal Rate of Substitution (MRS) is the rate at which a consumer can give up some amount of one good in exchange for another good while maintaining the same level of utility.)

"The MRT 1,2 measures the rate at which good 1 has to be given up to allow an increase in production of good 2. At the tangency point, the two gradients are equal so MRS_1,2 = MRT_1,2" p123-124

"Pareto efficiency judges an allocation by considering whether it is possible to undertake a reallocation of resources that can benefit at least one consumer without harming any. If it were possible to do so, then there would exist unexploited gains." p125

"The welfare properties of the economy, which are commonly known as the *Two Theorems of Welfare Economics*, are the basis for claims concerning the desir- ability of the competitive outcome. In brief, the First Theorem states that a competitive equilibrium is Pareto efficient and the Second Theorem that any Pareto efficient allocation can be decentralized as a competitive equilibrium." p126

"Any practical value of the Second Theorem depends on being able to achieve these required income levels. The way in which the theorem sees this as being done is by making what are called *lump-sum transfers* between consumers." p131

"Lump-sum transfers have a very special role in the theoretical analysis of public economics because, as we will show, they are the idealized redistributive instrument."p131-132